Lec 22 - Dimensions
Wednesday, February 29, 2012
9:30 AM
- A minimal spanning set of the vector space
- A maximal linearly independent set of the vector space.

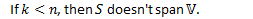

![]()
We can interpret a basis as:
Definition
![]()
![]()
Eg
![]()
![]()
![]()
![]()
Eg
![]()
![]()
![]() Theorem:
Theorem:
![]()
![]()
Proof of 3:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Q.E.D.
![]() Theorem:
Theorem:
![]()
Proof: A7
Eg
![]()
![]()
![]()
![]()
![]()
Eg
![]()
![]()
![]()
![]()
![]()
This gives a system of linear equations:
![]()
![]()
![]()
Row reduce the coefficient matrix:
![]()
Since rank of coefficient matrix equals the # of columns and the system Is consistent, the system has a unique solution.
![]()

![]()
![]() Coordinates
Coordinates
![]()
![]()
![]()
![]()
![]()
But we could also use another basis.
Eg
![]()
![]()
![]()
Definition
![]()

Note: Order of basis vectors matters.
Eg
![]()
![]()
![]()
![]()
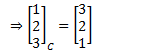
Eg
![]()
![]()
![]()